Hey! I'm Shreyas. I'm a Master's student (Dual Degree B.Tech. + M.Tech.) at the Center for Systems and Controls, Indian Institute of Technology Bombay, India. I finished my B.Tech. in Aerospace Engineering in April 2025. My research interests include geometric mechanics, control theory, optimization on manifolds, and nonlinear dynamical systems.
I also love hands-on projects, especially real-world applications involving aerial robotics, aeroelasticity, and control systems. I've recently also started working on data-driven control, and I'm a coffee buff :)
Warning
Problem: The current name of your GitHub Pages repository ("Solution: Please consider renaming the repository to "
http://".
However, if the current repository name is intended, you can ignore this message by removing "{% include widgets/debug_repo_name.html %}" in index.html.
Action required
Problem: The current root path of this site is "baseurl ("_config.yml.
Solution: Please set the
baseurl in _config.yml to "Education
-
Indian Institute of TechnologyCenter for Systems and Controls
Master's StudentMay 2025 - present -
Indian Institute of TechnologyB. Tech. in Aerospace EngineeringMay 2021 - Apr. 2025
Experience
-
ICMATResearch InternMay 2024 - Jul. 2024
News
Selected Publications (view all )
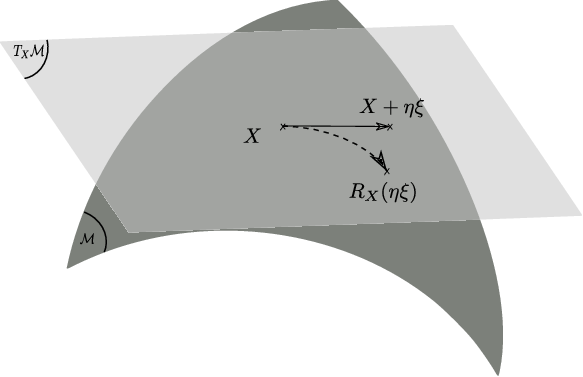
Feedback Linearizable Discretization of Second-Order Mechanical Systems
Shreyas N. B., David Martin de Diego, Ravi N. Banavar
European Controls Conference 2025
Mechanical systems are most often described by a set of continuous-time, nonlinear, second-order differential equations (SODEs) of a particular structure governed by the covariant derivative. The digital implementation of controllers for such systems requires a discrete model of the system and hence requires numerical discretization schemes. Feedback linearizability of such sampled systems, however, depends on the discretization scheme employed. In this article, we utilize retraction maps and their lifts to construct feedback linearizable discretizations for SODEs which can be applied to many mechanical systems.
Feedback Linearizable Discretization of Second-Order Mechanical Systems
Shreyas N. B., David Martin de Diego, Ravi N. Banavar
European Controls Conference 2025
Mechanical systems are most often described by a set of continuous-time, nonlinear, second-order differential equations (SODEs) of a particular structure governed by the covariant derivative. The digital implementation of controllers for such systems requires a discrete model of the system and hence requires numerical discretization schemes. Feedback linearizability of such sampled systems, however, depends on the discretization scheme employed. In this article, we utilize retraction maps and their lifts to construct feedback linearizable discretizations for SODEs which can be applied to many mechanical systems.
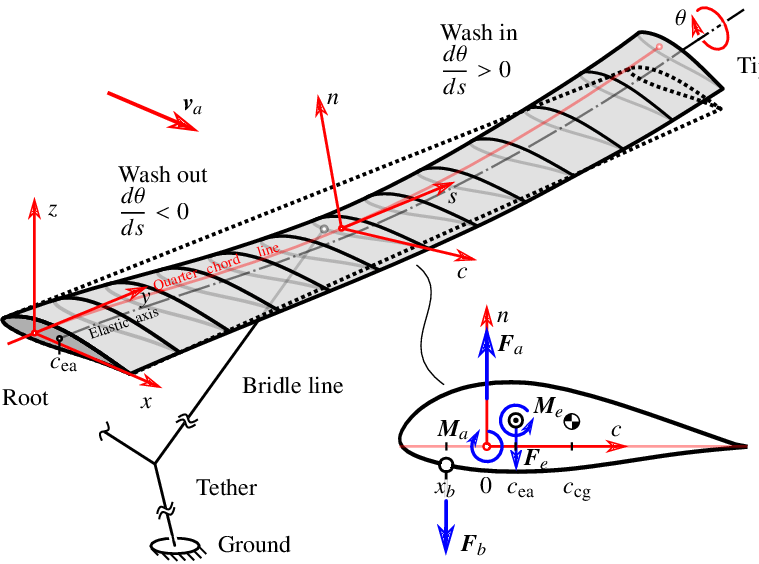
Nonlinear Infinite Dimensional Model for a Two Degree-of-Freedom Flexible WIng
Shreyas N. Bharadwaj, Vivek Natarajan, Aditya A. Paranjape
AIAA SciTech Forum 2025
An infinite-dimensional nonlinear model for a two-degree-of-freedom highly flexible wing is presented in this paper. The model describes the coupled dynamics of bending and torsion in terms of a set of nonlinear partial differential equations. When torsion is ignored, the resulting transverse bending equations are identical to those for the well-known elastica. The in vacuo response and the flutter onset characteristics of the model are compared with standard aeroelastic models using numerical simulation. The nonlinear model presented here could potentially serve as a benchmark for PDE-based control design methods, providing an intermediate step between low-fidelity linear models and nonlinear simulation models whose high fidelity is usually accompanied by large computational times.
Nonlinear Infinite Dimensional Model for a Two Degree-of-Freedom Flexible WIng
Shreyas N. Bharadwaj, Vivek Natarajan, Aditya A. Paranjape
AIAA SciTech Forum 2025
An infinite-dimensional nonlinear model for a two-degree-of-freedom highly flexible wing is presented in this paper. The model describes the coupled dynamics of bending and torsion in terms of a set of nonlinear partial differential equations. When torsion is ignored, the resulting transverse bending equations are identical to those for the well-known elastica. The in vacuo response and the flutter onset characteristics of the model are compared with standard aeroelastic models using numerical simulation. The nonlinear model presented here could potentially serve as a benchmark for PDE-based control design methods, providing an intermediate step between low-fidelity linear models and nonlinear simulation models whose high fidelity is usually accompanied by large computational times.